This is a tougher one, and honestly, you would have needed to have solved this yourself before to have gotten to a reasonable algorithm in the usual 1/2 hour time. It’s generally a significant sign if the problem description has to refer to Wikipedia for an accurate description of the problem.
This is one that is very simple to do by inspection, but difficult to do simply by algorithm, let alone an efficient one.
My first idea was that I’d need to know the paths to the nodes, and that I’d *handwave* figure out the common ancestor by using those. The good algorithm for this kind of uses the idea of paths to the nodes, but instead it does an in-order trace of the paths through the tree – an Euler tour, dude comes in everywhere – and that allows us to transform the problem into a range-minimum query (e.g., when I have node P and node q, and the path I needed to get from one to the other, at some point in there I’ll have a minimum-depth node, which will either be one of the two, or a third higher node).
The Wikipedia example shows this as an illustration:
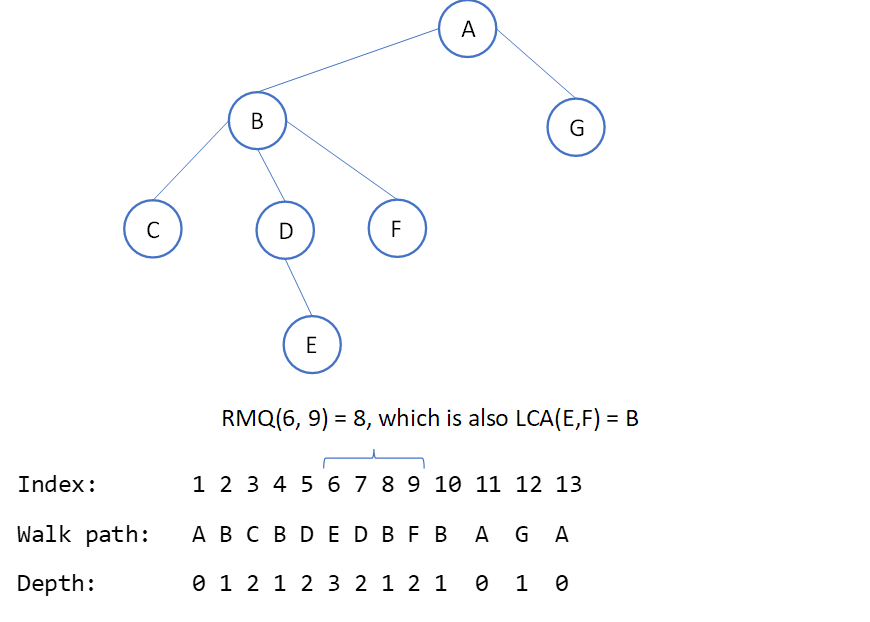
To spell this out more explicitly: you can see we did the in-order tour, transforming the tree into a linear walk through it: A, down to B, down to C, back up to B, down to D, down to E, up to D, and so on. We record the node value and the depth at each step. To get the range query, we want the first appearance of each of two nodes we’re searching for (and we can record that as we’re crawling), and then to look for the highest node in the range of nodes including both of them. For the example in the diagram, step 6 is where we find the first node, E, and step 9 is where we find the second node, F. Iterating from step 6 to step 9, the node with the lowest depth in that range is B, and we can see from inspecting the tree that this is correct.
So.
At this point I’ve explained the solution, but have not written any code for it at all yet. Better go get that done.
Note: I’ve gotten the Euler crawl to mostly work, but I’m having trouble with the returned data from the crawl. Debugging…and yes, I am too cheap to pay for leetcode’s debugger. fmt.Println FTW.
The crawler crawls, but the output is wrong. I’ve tracked this down to a fundamental error on my part: Go arrays are not built for this kind of thing. I am switching the crawler over to building a linked list, which I think I only have to traverse one direction anyway, so it’s just as good.
This definitely was a failure to time-block. I will keep plugging on this until I actually finish solving it, but this would have been a DQ in an interview.
I’ve now discarded two different Euler crawls, and have a working one…but the range-minimum isn’t working as I expect it to. Will have to come back to it again. I begin to wonder if trying to track the start node is, in fact, a bad idea, and if I should simply convert the linked list I’m generating in the crawl to an array for the range minimum once it’s returned.
The crawl now returns the head and tail of a list that contains the visit order for the Euler crawl: node, left subtree in order, node again, right subtree in order, node again. This breaks down like this:
If the current head is nil, return [nil, nil].
Generate a crawl node for just this node at the current level
Set head and tail to this node
If the current head points to a leaf node:
Return head and tail.
Otherwise:
Crawl the left side at level+1, getting a leftside head and tail.
Crawl the right side at level+1, getting a rightside head and tail.
If the leftside crawl is non-null:
Set tail.next to leftside head.
Create a new crawl node for the current node at the current level.
Set leftside tail node's next to this new node.
Set tail to this middle node.
If the rightside crawl is non-null:
Set tail.next to the rightside head.
Create a new crawl node for the current node at the current level.
Set rightside tail node's next to this new node.
Set tail to this new node.
Return head and tail.This returns a singly-linked list with an in-order traversal, recording every node visited and the tree level at which it was seen. We should now be able to find the start and end nodes, and scan the list between the two inclusive, looking for the highest node, and that should find the LCA.
The scan is a bit of a bastard as well. The nodes may appear in any order, and we have to find the start and end no matter which order they show up in. I initially tried swapping them if they were out of order, but this didn’t work as I expected – that may have been other bugs, but I coded around it in the final scan code.
The final scan first says “I don’t have either node” and skips nodes until it finds one of them. Once it does, it starts looking for the node with the highest level. The tricky bit is that we need to detect that we’ve found the first node, then start checking, and only stop checking after we find the end node (as it may be the highest, since nodes are considered their own roots).
Here’s the final code. It did not do well in the rankings: bottom 5% in speed, and bottom 25% in memory usage. I suspect I could improve it by merging the “find the local high node” code into the Euler crawl, and by not actually recording the nodes in the linked list at all but passing the state around in the recursion.
Lessons learned:
- Do not try to do complicated array machinations in Go. Better to record the data in a linked list if you’re doing something that needs to recursively append sublists.
- Think more clearly about recursion. What is the null case? What is the one-element case? What is the more-than-once case? What is the termination criterion for the more-than-one case?
- Don’t be afraid to discard an old try and do something different. Comment out the failed code (and note to the interviewer that you’d check the broken one in on a local branch in case you wanted to go back to it).
- Continuing to practice with Go pointer code is necessary. I’m a bit weak with pointers.
This took way too long to do, and way too many shots at getting to something that would work at all. I grade myself a fail on this one. I might come back at a later date and try to make it faster and smaller.
Addendum: removed the debugging and the dump of the crawl output. Even without doing anything else, that bumped my stats to the top 73% in runtime and top 99% in memory usage, and that is a pass with flying colors!
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
type eulerNode struct {
node *TreeNode
depth int
next *eulerNode
}
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
// Use the transformation of this problem into a range-minimum one.
// Crawl the tree in-order, creating an Euler path. Each step records
// the node value and the depth.
head, tail := eulerCrawl2(root, p, q, 0)
// dump crawl output - note that removing this should make the code
// significantly faster
scan := head
for {
if scan == nil {
break
}
fmt.Println(scan.node.Val, "depth", scan.depth)
scan = scan.next
}
fmt.Println("crawl complete", head, tail)
// Start is the beginning of the range, and the end of the path is the end.
// Find the path minimum in the range (the lowest depth value).
var ancestor *TreeNode
minDepth := 9999999999
fmt.Println("Start at", head.node.Val, head.depth)
foundP := false
foundQ := false
for scan := head; scan != nil; scan = scan.next {
fmt.Println("node", scan.node.Val, scan.depth)
if scan.node.Val == p.Val {
fmt.Println("found p")
foundP = true
}
if scan.node.Val == q.Val {
fmt.Println("found q")
foundQ = true
}
if !foundP && !foundQ {
fmt.Println("skip", scan.node.Val)
continue
}
fmt.Println("check", scan.node.Val, scan.depth)
if scan.depth < minDepth {
// New range minimum
minDepth = scan.depth
ancestor = scan.node
fmt.Println("new candidate min at", scan.node.Val, scan.depth)
}
if foundP && foundQ {
fmt.Println("found and processed complete range")
break
}
}
fmt.Println("ancestor is", ancestor.Val)
return ancestor
}
func eulerCrawl2(root, p, q *TreeNode, depth int) (*eulerNode, *eulerNode) {
// Nil tree returns nil pointer
if root == nil {
fmt.Println("skipping nil pointer")
return nil, nil
}
// Non-nil next node. Generate a crawl node for this tree node.
fmt.Println("adding crawl node for", root.Val)
head := &eulerNode{
node: root,
next: nil,
depth: depth,
}
tail := head
// If this is a leaf, the crawl of
// this node is just this node. Head and tal point to the same node.
if root.Left == nil && root.Right == nil {
fmt.Println("returning at leaf")
return head, tail
}
// Non-leaf. Crawl will be this node, the left subtree at depth+1,
// another copy of this node at this depth, the right subtree at depth+1,
// and one more copy of this node.
fmt.Println("crawling down")
leftSubtreeHead, leftSubtreeTail :=
eulerCrawl2(root.Left, p, q, depth+1)
rightSubtreeHead, rightSubtreeTail :=
eulerCrawl2(root.Right, p, q, depth+1)
// Chain the results together:
// - this tree node
// - the left crawl below it
// - another copy of this node
// - the right crawl below it
// - a final copy of this node
// Link this node to the start of the list from the left crawl
if leftSubtreeHead != nil {
// If there is a crawl below, link it in, and add another
// copy of the current node for coming back up
tail.next = leftSubtreeHead
leftSubtreeTail.next = &eulerNode{
node: root,
next: nil,
depth: depth,
}
tail = leftSubtreeTail.next
}
if rightSubtreeHead != nil {
// right crawl exists. Add it at the current tail, reset tail.
tail.next = rightSubtreeHead
rightSubtreeTail.next = &eulerNode{
node: root,
next: nil,
depth: depth,
}
// reset tail to new last node
tail = rightSubtreeTail.next
}
// Return head and tail of the newly-generated list of crawled
// nodes.
fmt.Println("returning results at depth", depth)
return head, // Head of this new list
tail // Tail of this new list
}
Leave a Reply
You must be logged in to post a comment.